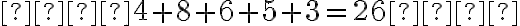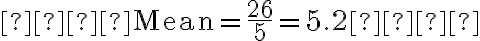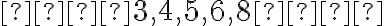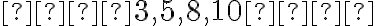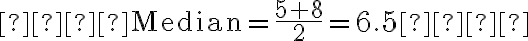g6abesept7: G7 - Mathematics - Mean, Median, Mode, and Range - Lesson Notes

# Chapter: Measures of Central Tendency and Dispersion

In mathematics, especially in statistics, we often encounter sets of numbers. To understand these numbers better, we use certain measures that help us summarise and describe data. Four fundamental measures are the **mean**, **median**, **mode**, and **range**. Each of these measures provides different insights into the data set. Let’s explore each one in detail.

## Mean

The **mean** is often referred to as the average. It is calculated by adding up all the numbers in a data set and then dividing by the total number of values. The mean gives us a central value of the data.

### How to Calculate the Mean

1. **Add all the numbers together.**

2. **Divide the total by the number of values.**

### Example

Consider the following set of numbers: 4, 8, 6, 5, and 3.

1. First, add the numbers together:

$4 + 8 + 6 + 5 + 3 = 26$

2. There are 5 numbers in this set.

3. Now, divide the total by the number of values:

$\text{Mean} = \frac{26}{5} = 5.2$

So, the mean of this set of numbers is **5.2**.

### Analogy

Think of the mean as sharing a pizza equally among friends. If you have a pizza with 8 slices and 4 friends, each friend would get 2 slices. In this way, the mean represents an equal share of the total.

## Median

The **median** is the middle number in a data set when the numbers are arranged in order. If there is an even number of values, the median is the average of the two middle numbers.

### How to Calculate the Median

1. **Arrange the numbers in ascending order.**

2. **Find the middle number.** If there are an odd number of values, the median is the middle one. If there are an even number, calculate the mean of the two middle numbers.

### Example

Using the same set of numbers: 4, 8, 6, 5, and 3.

1. First, arrange the numbers in order:

$3, 4, 5, 6, 8$

2. Since there are 5 numbers (an odd amount), the median is the middle number, which is **5**.

Now, let’s consider a different set: 3, 5, 8, and 10.

1. Arrange the numbers:

$3, 5, 8, 10$

2. There are 4 numbers (even), so the median is the average of the two middle numbers (5 and 8):

$\text{Median} = \frac{5 + 8}{2} = 6.5$

So, the median of this set is **6.5**.

### Analogy

Think of the median like finding the middle seat in a row of chairs at a theatre. If you have an odd number of chairs, there’s one clear middle seat. If there’s an even number, you might have to choose between the two middle seats.

## Mode

The **mode** is the number that appears most frequently in a data set. A data set may have one mode, more than one mode, or no mode at all.

### How to Calculate the Mode

1. **Count how many times each number appears.**

2. **Identify the number(s) that appear most often.**

### Example

Consider the numbers: 2, 4, 4, 6, 7, 8.

1. Count the occurrences:

- 2 appears 1 time

- 4 appears 2 times

- 6 appears 1 time

- 7 appears 1 time