Compound Proportions and Rates of Work Lesson Notes
In mathematics, particularly in the study of ratios and proportions, we encounter the concept of **compound proportions**. This concept is essential when dealing with multiple quantities that change in relation to one another. Understanding compound proportions is crucial for solving problems that involve rates of work, mixtures, and other scenarios where different elements interact.
What are Proportions?
A **proportion** is an equation that states that two ratios are equal. For example, if we say that the ratio of boys to girls in a classroom is 2:3, we can express this as: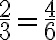
This means that for every 2 boys, there are 3 girls, and we can multiply both sides of the equation by the same number to maintain equality.
Compound Proportions
**Compound proportions** involve more than one ratio or proportion, where multiple variables are interconnected. This can be represented as follows:
If 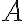 is to
is to 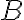 as
as 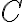 is to
is to 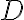 , we can write this as:
, we can write this as: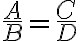
In practical terms, this means that the relationship between 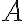 and
and 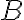 is proportional to the relationship between
is proportional to the relationship between 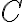 and
and 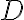 .
.
### Example of Compound Proportions
Let’s consider a real-world example involving a recipe. Suppose a recipe requires 2 cups of flour for every 3 cups of sugar. If we want to find out how much flour we need for 9 cups of sugar, we can set up the proportion:
To solve for 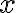 , we cross-multiply:
, we cross-multiply: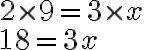
Dividing both sides by 3 gives: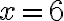
Thus, we need 6 cups of flour for 9 cups of sugar. This exemplifies how compound proportions work in a practical scenario.
## Rates of Work
The concept of **rates of work** is often associated with compound proportions when dealing with jobs completed by multiple workers or machines. A rate of work is typically expressed as the amount of work done per unit of time.
### Understanding Rates of Work
When we say one worker can complete a task in a specific time, we can express their work rate. For example, if Worker A can paint a wall in 4 hours, their rate of work is: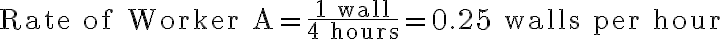
If Worker B can paint the same wall in 2 hours, their work rate is: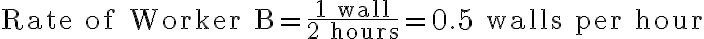
### Combining Rates of Work
When multiple workers collaborate, we can combine their rates to find the total work rate. For example, if Workers A and B work together, their combined rate of work is:
### Example of Rate of Work
Let’s say a project requires the painting of 3 walls, and we want to know how long it will take for Workers A and B to complete the job together.
We can use the combined rate: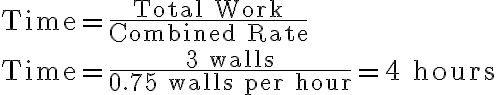
Thus, it will take them 4 hours to complete the painting of 3 walls when working together.
## Conclusion
In summary, understanding compound proportions and rates of work is essential for solving various mathematical problems. Compound proportions allow us to establish relationships between multiple quantities, while rates of work help us determine how efficiently tasks can be completed when multiple workers are involved. By applying these concepts, we can tackle complex problems in mathematics and real-life scenarios effectively.
Background Colour
Font Face
Font Kerning
Font Size
Image Visibility
Letter Spacing
Line Height
Link Highlight
Text Colour
Text Alignment
Paragraph Width
